These CAT Sequence and Series questions/problems with solutions provide you vital practice for the topic. The purpose of these posts is very simple: to help you learn through practice.
Question 1: Find the following sum>
1/(22 –1) +1/(42 –1) + 1/(62 –1) + …. +1/(202 –1)
(a) 9/10
(b) 10/11
(c) 19/21
(d) 10/21
Answers and Explanations

Question 2: Two men X and Y started working for a certain company at similar jobs on January 1, 1950. X asked for an initial salary of Rs. 300 with an annual increment of Rs. 30. Y asked for an initial salary of Rs. 200 with a rise of Rs. 15 every six months. Assume that the arrangements remained unaltered till December 31, 1959. Salary is paid on the last day of the month. What is the total amount paid to them as salary during the period?
(a) Rs. 93,300
(b) Rs. 93,200
(c) Rs. 93,100
(d) None of these
Question 3: Let S denote the infinite sum 2 + 5x + 9x2 + 14x3 + 20x4 + …, where | x | < 1, then S equals
(a) {(2-x)/(1-x)3}
(b) {(2-x)/(1+x)3}
(c) {(2+x)/(1-x)3}
(d) {(2+x)/(1+x)3}
Question 4: The infinite sum 1 + (4/7) + (9/72) + (16/73) + (25/74) + …. equals
(a) 27/14
(b) 21/13
(c) 49/27
(d) 256/147
Question 5: Consider the set S = (1, 2, 3, …, 1000}. How many arithmetic progressions can be formed from the elements of S that start with 1 and end with 1000 and have at least 3 elements?
(a) 3
(b) 4
(c) 6
(d) 7
(e) 8
Answers and Explanations
Answers: (d)
Let number of terms in the arithmetic progression be n, then
1000 = 1 + (n–1) d
=>(n–1) d = 999
=> n – 1 = 999/d
Since n is an integer, so n – 1 is also an integer. This means that ‘d’ is a factor of 999.
Now 999 = 33 × 37. so the total factors of 999 are 4 × 2 = 8.
Out of these 8 factors one factor is 999 and we will reject it as in that case there will be only two terms in the
A.P. i.e. 1 and 1000, which is not possible.
Hence, ‘d’ can take 7 different values.
So, in total, 7 A.Ps. are possible.




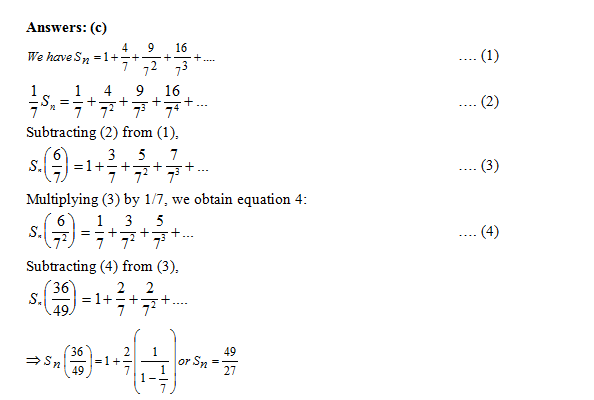
















Amazing explanation thank you!!